Paul Bungartz und Alexander Wynands April 1999
Wie beurteilen Referendare ihr Mathematikstudium für das Lehramt Sek II?
Es erfolgte hierzu im Sommer 1998 eine Befragung von Referendarinnen und Referendaren für Mathematik an 11 Studienseminaren für die Sekundarstufe II (Sek. II) in NRW. Die Fragebögen sind (im Anhang) beigefügt.
Angeregt wurde unsere Befragung u.a. durch Diskussionen im Mathematischen Institut der Universität Bonn über Form und Inhalt der Ausbildung von Mathematiklehrern für die Sek. II. Dieser Bericht ist deskriptiv, nur an wenigen Stellen vorsichtig wertend oder fragend. Er enthält die gestellten Fragen an die Referendare und Fachleiter und eine Auswertung der Antworten. Die Auswertung erfolgte mit SPSS.
Zusammenfassung.
Ihr Studium für das Lehramt in Mathematik in der Sekundarstuf II bewerten Referendarinnen und Referendare sehr kritisch.
Dank
Bedanken möchten wir uns vor allem bei den Seminarleitern, den Fachleitern und den Referendaren, die diese Untersuchung mitgetragen haben. Dank gilt auch Herrn E. Ch. Wittmann, der uns zu dieser Untersuchung sehr ermutigt hat. Sein zusammen mit Bettina Seipp als Info, Ausgabe 2 (Mai 1997) im "Zentrum für Lehrerausbildung" , Uni. Dortmund veröffentlichter Bericht: "Grundschullehrer(innen)-Ausbildung zwischen Fachwissenschaft, Fachdidaktik und Praxis" gab Anregungen für einige auch bei uns gestellte Fragen. Danken möchten wir auch Uwe Tietze, Göttingen für seine Unterstützung. Die Frage nach den für zukünftige Mathematiklehrer in der Sekundarstufe II (Gymnasium) gewünschten Themen haben wir (modifiziert) einer von ihm geleiteten Untersuchung entnommen.
Probanden
Beantwortet haben 176 Referendare die Fragen nach Qualität und Inhalt ihres Studiums.
Die Frage nach ihrem Alter beantworteten 174:
90 Frauen zwischen 25 und 40 Jahren. Durchschnittsalter 27,6 Jahre; 8 waren älter als 30 Jahre.
84 Männer zwischen 25 und 40 Jahren. Durchschnittsalter 29,3 Jahre; 20 waren älter als 30 Jahre.
Von 12 Fachleitern für Mathematik wurden die an sie gerichteten Fragen beantwortet. Die sich darauf beziehenden Ergebnisse sind in diesem Bericht kursiv gedruckt.
Die 176 Referendare waren auf die 11 Seminare folgendermaßen verteilt:
| Stadt | Bielefeld | Bonn | Duisburg | Düsseld. | Essen | Kleve | Köln | Münster | Paderborn | Siegburg | Wuppert |
| Anzahl Refer. | 8 | 21 | 14 | 16 | 20 | 20 | 7 | 25 | 24 | 9 | 12 |
Von den Referendaren hatten ihr 1. Staatsexamen bestanden an der Universität / Gesamthochschule...
Münster 41 Bonn 24 Köln 16 Paderborn 11
Düsseldorf 9 Bochum, Osnabrück, Wuppertal je 8, Essen 6, Bielefeld, Dortmund, Oldenburg je 5.
Weitere 18 Universitäten / Gesamthochschulen waren mit weniger als 5 Absolventen vertreten.
Die Frage nach dem Termin ihres 1. Staatsexamens beantworteten 167 Referendare:
55% der Referendare hatten ihr 1. Staatsexamen 1996, 38% hatten es 1997 bestanden. Die Mehrzahl der Befragten war also bereits im 2. Referendarjahr. 12 Referendare hatten vor 1996 ihr Examen gemacht, d.h. sie hatten Wartezeiten zu überbrücken (oder eine "verlängerte" Referendarzeit).
Die SPSS-Tabelle zeigt genauere Angaben:

Als 2. Unterrichtsfach gaben 53% Physik, Chemie, Biologie oder Informatik an. 20% hatten Sport, Erdkunde oder Geschichte, 11% Deutsch oder eine Fremdsprache. Viele Referendare studierten im Zweitfach keine Naturwissenschaft oder Informatik, was eine "Studienorganisation" häufig erschweren kann.
Von den 12 Fachleitern für Mathematik, die zwischen 1964 und 1991 ihr 1. Staatsexamen ablegten, hatten 7 Physik als 2. Studien- bzw. Unterrichtsfach. Als weitere 2. Fächer wurden Informatik, Geographie, Sport, Philosophie und Sozialwissenschaft genannt.
Nur jeder 5. Referendar mit dem studierten Unterrichtsfach Mathematik hatte in Mathematik seine Staatsexamensarbeit (Hausarbeit) geschrieben. Bei 9 von diesen 34 Referendaren hatte diese Arbeit (eher oder sehr) "wohl Relevanz für die Tätigkeit als Lehrer". Von den 39 (22%) Arbeiten, die in Physik, Chemie, Biologie oder Informatik geschrieben wurden, hatten 14 "Relevanz für die Tätigkeit als Lehrer".

Insgesamt hatte für ca. 70% das Thema der Hausarbeit "gar nicht" oder "eher nicht" Relevanz für ihre spätere Lehramtstätigkeit. Der Anteil "relevanter Hausarbeits-Themen für das Berufsfeld Lehrer" ist an den Hochschulen recht unterschiedlich: In Paderborn waren es 5 von 11, in Münster 12 von 41, in Bonn 4 von 24 und in Köln 2 von 16.
Es ist erstaunlich (!?), daß so wenige Arbeiten (20%) in Mathematik geschrieben werden, obwohl die "Beliebtheit" der studierten Unterrichtsfächer nahezu gleich ist: Lieblingsfach Mathematik 45%, beide gleich 5%.
Für 10 von 12 Fachleitern, die den ihnen zugedachten Fragebogen zurückschickten, hatte ihre eigene Hausarbeit "keine Relevanz für die spätere Tätigkeit als Lehrer"; 7 meinten, es sollte nicht "grundsätzlich eine fachwissenschaftliche Arbeit" sein; 10 Fachleiter meinten, sie "kann sowohl fachinhaltliche als auch fachdidaktische Schwerpunkte haben"
Hier einige "freie Kommentare" zu den eigenen Hausarbeitsthemen:
| * leider (keine Relevanz) |
| * Meromorphe Funktionen sind schulisch nicht brauchbar. |
| * Es war ein Gebiet aus der Homologischen Algebra, das absolut keine Beziehung zur Lehrtätigkeit hatte. |
| * Da beide Schwerpunkte wichtig sind und der 2. die Referendarzeit prägt, sollte der erste unbedingt im Rahmen des Fachstudiums angemessen vertreten sein. |
| * Thema: "Anpassung des Lehrers" (Praxisschock) |
Qualität des Studiums
Frage 1.1: Wie beurteilen Sie die Qualität Ihres Grundstudiums als Basis für Ihre Ausbildung als Mathematiker(in) und Lehrer(in)?
Für eine Maßskale zur "Mittelwertbildung" werden die angekreuzten Antworten (von links nach rechts) mit den Werten 1(sehr schlecht), 2(eher schlecht), 3(eher gut) bzw. 4(sehr gut/richtig angemessen) kodiert.
| Die meisten (63%)
bewerten die Qualität ihres Grundstudiums sehr / eher
schlecht. Der Mittelwert aller Antworten zur Frage 1.1 ist 2,31. Bonn und Köln werden nicht ganz so schlecht bewertet. |
 |
SPSS-Tabelle zu Frage 1.1:
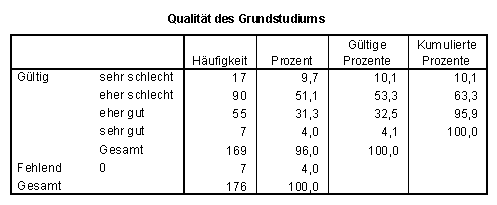
Viele, für die zu hohe Anforderungen im Grundstudium gestellt wurden, bewerten –gerade deshalb!?- die Qualität des Grundstudiums als "eher oder sehr schlecht". Sie verstehen zu wenig und das finden sie schlecht. Dies zeigt die SPSS-Kreuztabelle:

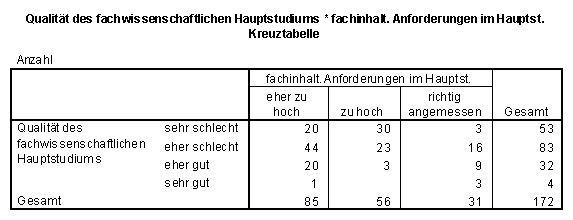
Frage 2.1: Qualität des fachwissenschaftlichen Hauptstudiums
| Mit 79%
bewerten noch mehr die Qualität ihres Hauptstudiums als
die des Grundstudiums als sehr / eher schlecht. Bei einem Gesamt-Mittelwert von 1,92 wird Bonn mit 2,12 besser bewertet als die übrigen 3 Unis, von denen mehr als 10 Probanden kamen. |
 |
SPSS-Tabelle zu Frage 2.1:

Noch deutlicher als bei der Bewertung des Grundstudiums gilt hier:
Die Qualität des Hauptstudiums bewerten viele, für die zu hohe Anforderungen gestellt werden, als "eher oder sehr schlecht". Dies zeigt die SPSS-Kreuztabelle:
Frage 3.2: Wie beurteilen Sie die Qualität der von Ihnen besuchten Veranstaltungen zur Mathemathikdidaktik im Hinblick auf Ihre Berufsvorbereitung als Lehrer(in)?
| Mit 83% bewerten die Befragten die Qualität der fachdidaktischen Veranstaltungen ebenso schlecht wie die der fachinhaltlichen ihres Hauptstudiums. Der Gesamt-Mittelwert ist 1,77. Bonn wird mit 2,17 deutlich besser bewertet als die übrigen 3 Unis in der Vergleichstabelle. | 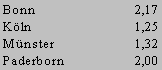 |
SPSS-Tabelle zu 3.2:

Sehr unterschiedlich ist offensichtlich an den Universitäten / Gesamthochschulen das Angebot bzw. die Teilnahme der Studierenden an mathematikdidaktischen Veranstaltungen insbesondere an Schulpraktischen Studien (Fachdidaktischen Praktika).
Während in Bonn nur 2 von 24 Probanden keine Veranstaltungen zu allgemeinen fachdidaktischen Problemen des MU besuchten (vgl. Frage 3.1), 5 Probanden keine zum "Stoff" der Sek II und nur 1 Proband keine zum "Stoff" der Sek I, sind die Zahlen für Köln und Münster doch sehr bedenklich niedrig. Besonders nachdenklich macht, daß nur etwa jeder zweite Studierende in Münster an Schulpraktischen Studien (vgl. Frage 3.4) teilgenommen hat.
Die Tabelle zeigt die Anzahlen der Referendare, die an der Hochschule in ..., die Veranstaltungen besuchten zu ...
| In... | #Probanden | allg. fachdid. | Stoff Sek II | Stoff Sek I | SchulPraktik. |
| Bonn | 24 |
22 |
19 |
23 |
22 |
| Köln | 16 |
9 |
6 |
2 |
14 |
| Münster | 41 |
12 |
16 |
8 |
22 |
| Paderborn | 11 |
8 |
10 |
9 |
11 |
| Gesamt | 176 (100%) |
112 (64%) |
105 (61%) |
92 (53%) |
122 (70%) |
Es drängen sich hier viele Fragen auf, z.B.:
Wie wichtig nehmen Studierende und Dozierende eine fachdidaktische Vorbereitung von Lehramtskandidaten in der 1. Ausbildungsphase?
Wie weit liegen Prüfungsordnungen und Studienordnungen in ihren Sollwerten entfernt von den Istwerten?
Worin wird ein Kandidat in einer Zusatzprüfung für das Lehramt für die Sekundarstufe I geprüft? Von wem?
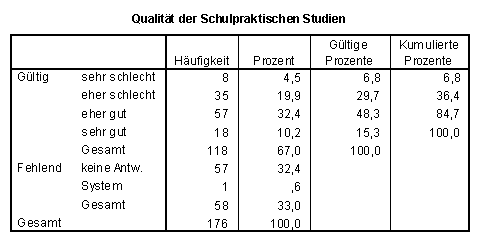
Frage 3.4: Qualität der Schulpraktischen Studien
| Mit ca. 64% bewerten die Referendare ihre Schulpraktika als "eher / sehr gut". Bonn liegt hier mit 2,91 bei einem Mittelwert von 2,72 für die Qualität und mit einem sehr hohen Teilnehmeranteil "vorne". | 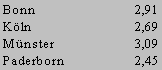 |
SPSS-Tabelle zu Frage 3.4:
Frage 3.7: Qualität der Erziehungswissenschaftlichen Studien
| Die Bewertung
dieses Studienanteils ist an allen Universitäten sehr
schlecht: 88% halten die Erziehungsw. Studien für "sehr
/ eher schlecht". Die beste Beurteilung erhielt hier
von den 4 Vergleichsunis Paderborn. Der Gesamt-Mittelwert ist 1,74 |
 |
SPSS-Tabelle zu Frage 3.7:
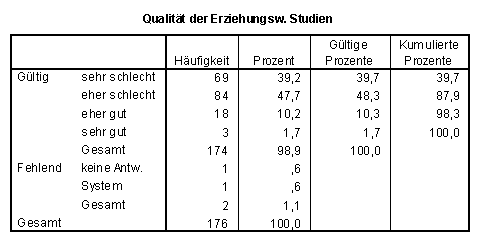
Frage 4.1: Das Mathematikstudium sollte mathematische Kompetenz und Selbstvertrauen vermitteln
| Trotz der geäußerten Kritik geben 71% der Probanden an, ihre mathematische Kompetenz sei durch das Studium "recht gut / sehr gut" geworden. Der Mittelwert liegt mit 2,84 höher als alle anderen "Qualitäts-Mittelwerte" |  |
Es drängt sich die Frage auf, ob es nicht zu viele (28%) gibt, bei denen das fachinhaltliche Ziel des Studiums "gar nicht / eher nicht" erreicht scheint.
SPSS-Tabelle zu Frage 4.1

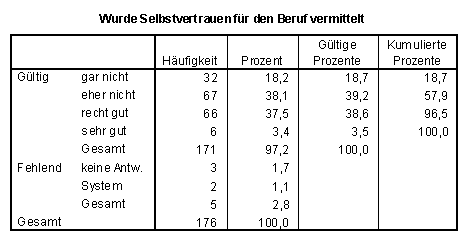
Mit der Einschätzung der mathematischen Kompetenz korreliert sehr stark das Selbstvertrauen, das im Studium für den angestrebten Beruf erreicht wurde. Es ist zu hoffen, daß manche Probanden eher bescheiden als selbstsicher geantwortet haben.
| Nur 42 %
glauben, daß ihr Mathematikstudium ihnen "recht
gutes / sehr gutes" Selbstvertrauen vermittelt hat. Oder: mehr als die Hälfte äußert zu gering entwickeltes Selbstvertrauen. Der Gesamt-Mittelwert liegt bei 2,27. |
 |
SPSS-Tabelle zu Frage 4.1:
Mit den Mittelwerten für die 7 vorgenannten Qualitätsmerkmale ergibt sich folgende
"Rangliste" der 4 Universitäten, von denen mehr als 10 Referendare kamen.
| Universität / Gesamthoch. | #Probanden | Grund-studium | Haupt-studium | Didaktik | SchulPrakt. | Zw.Summe | ErzieWiss. | Zw.Summe | Fach- Kompet. |
Selbst-vertrauen | Summe |
| Bonn | 24 |
2,43 |
2,12 |
2,17 |
2,91 |
9,63 |
1,33 |
10,96 |
2,96 |
2,35 |
16,27 |
| Münster | 41 |
2,24 |
1,93 |
1,32 |
3,09 |
8,58 |
1,68 |
10,26 |
2,83 |
2,26 |
15,35 |
| Paderborn | 11 |
2,09 |
1,64 |
2,00 |
2,45 |
8,18 |
1,91 |
10,09 |
2,45 |
2,18 |
14,72 |
| Köln | 16 |
2,50 |
1,38 |
1,25 |
2,69 |
7,82 |
1,27 |
9,09 |
3,13 |
2,44 |
14,66 |
| Gesamt | ca. 170 |
2,31 |
1,92 |
1,77 |
2,72 |
8,72 |
1,74 |
10,46 |
2,84 |
2,27 |
15,57 |
Grundstudium – Fragen 1.2 bis 1.5
Die meisten Befragten (ca. 70%) finden ein gemeinsames Grundstudium mit Diplom-Mathematik-Studenten "(sehr / eher) schlecht" (vgl. Frage 1.2).
Nur 3 von 11 antwortenden Fachleitern sind
gegen ein gemeinsames Grundstudium von Mathematik-Lehramtskandidaten
für die Sekundarstufe II zusammen mit Diplomkandidaten. Hierzu
einige Antworten:
* Dies "ja" gilt speziell für Lehramtskandidaten Sek.
II
* Gemeinsame Organisation, um gegebenenfalls einen Wechsel zu ermöglichen.
* ja, kann nicht schaden.
SPSS-Tabelle zu 1.2:
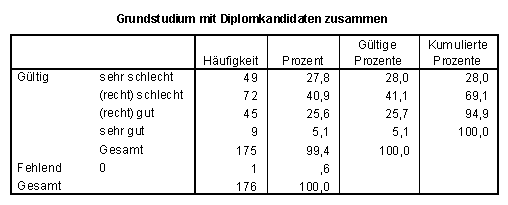
Die fachinhaltlichen Anforderungen im Grundstudium (vgl. Frage 1.3) finden 70% "(eher) zu hoch". Etwa 28% halten diese für "richtig angemessen".
SPSS-Tabelle zu Frage 1.3:

Noch mehr Referendare (ca. 85%) halten die Übungsaufgaben zu den Vorlesungen für "(eher) zu schwer" (vgl. Frage 1.4). Nur 15% halten sie für "richtig angemessen".
SPSS-Tabelle zu Frage 1.4:
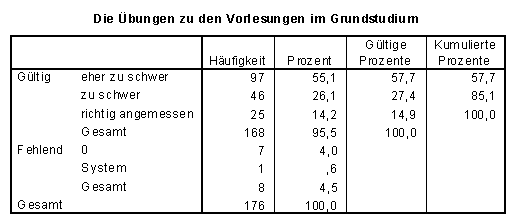
Klausuren (am Semesterende) zu den Pflichtveranstaltungen können zur Selbsteinschätzung, Studienorientierung und zu Erfahrungen bei schriftlichen Prüfungen beitragen. Nur 6% möchten auf keinen Fall" auf solche Klausuren verzichten. Mit 42% ist der Anteil derjenigen, die "auf jeden Fall" solche Klausuren befürworten recht hoch.
SPSS-Tabelle zu Frage 1.5:
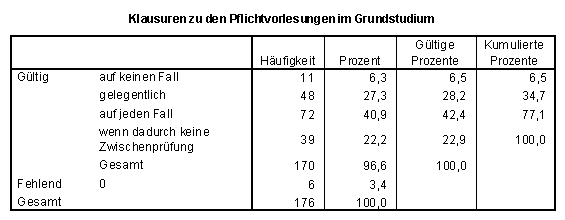
Hauptstudium – Fragen 2.2 bis 2.4
Im fachwissenschaftlichen Studium finden ca. 90% das Berufsfeld des Lehrers "gar nicht oder zu wenig" berücksichtigt (vgl. Frage 2.2)
Von den 12 Fachleitern meinten 7 das Berufsfeld des Lehrers sollte "häufig" berücksichtigt werden, 4 betonten es solle "sehr stark" berücksichtigt werden. Einige (freie) Kommentare:
* Hier gilt es, eklatante Lücken zu schließen.
* Anwendungsbezüge herstellen!
* Referendare haben keinen Überblick über die Inhalte der Schulmathematik.
SPSS-Tabelle zu Frage 2.2:

Etwa 82% halten die fachinhaltlichen Anforderungen im Hauptstudium für Lehramtskandidaten für "(eher) zu hoch"; 18% halten sie für "richtig angemessen", das sind 10% weniger als bei der entsprechenden Frage zum Grundstudium (vgl. Frage 2.3 und 1.3).
SPSS-Tabelle zu Frage 2.3:
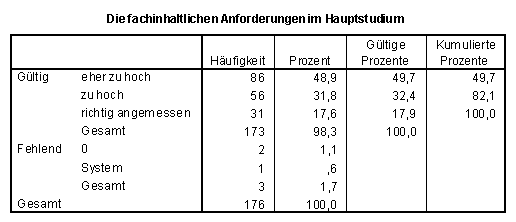
Befürwortet werden von fast allen Lehramtsstudenten spezielle fachinhaltliche Veranstaltungen getrennt von Diplomkandidaten (vgl. Frage 2.4)
SPSS-Tabelle zu Frage 2.4:

Mathematikdidaktik und Erziehungswissenschaft – Frage 3.1 bis 3.7
Der Anteil der Referendare, die keine Veranstaltung zu mathematikdidaktischen - allgemeinen oder stoffinhaltlichen – Problemen besucht haben ist (zu ) hoch (vgl. Frage 3.1).
39% haben nichts über stoffinhaltliche Fragen zum Mathematikunterricht der Sekundarstufe II in Veranstaltungen erfahren; 46% nichts über stoffinhaltliche Probleme der Sekundarstufe I.
SPSS-Tabellen zu Frage 3.1:
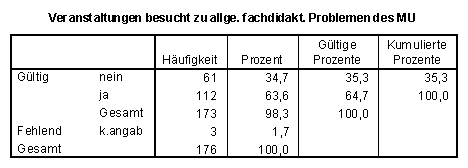
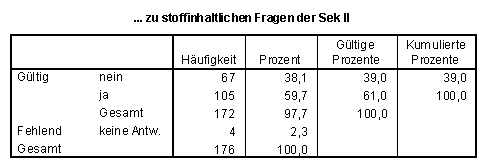
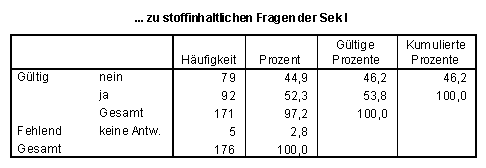
Viele möchten wesentlich mehr als möglich war selbständig aktiv in fachdidaktischen Veranstaltungen unterrichtspraktische Probleme bearbeiten (vgl. Frage 3.3). Nur 10% hatten dazu häufiger Gelegenheit.
SPSS-Tabelle zu Frage 3.3:

Schulpraktische Studien (vgl. Frage 3.4) sind verpflichtender Bestandteil der Prüfungsordnung bzw. Studienordnung. Aber: Fast jeder Dritte der Befragten hat in der 1. Ausbildungsphase nicht daran teilgenommen. Ist das ein akzeptabler Istzustand?
Unterrichtspraktische Erfahrung von Lehramtskandidaten für die Sek. II halten 7 ( von 12) befragte Fachleiter für "sehr wichtig", 4 für "wichtig" und einer für "weniger wichtig". Kommentare der Fachleiter dazu:
* "Wichtig scheint mir hier weniger der Ausbildungsaspekt als die Möglichkeit, die eigene grundsätzliche Eignung zu überprüfen".
* "ungeeignete können den Studiengang wechseln".
* "Sie sollten zu einem frühen Zeitpunkt des Studiums möglich sein, um eventuelle Nichteignung früh festzustellen".
SPSS-Tabellen zu Frage 3.4:
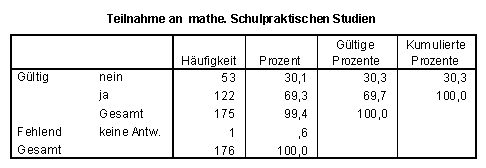
Mehr als 80% derjenigen, die ein solches Praktikum mitmachten, halten den ihnen gebotenen Umfang für zu gering. (Zur Qualitätseinschätzung s.o.)
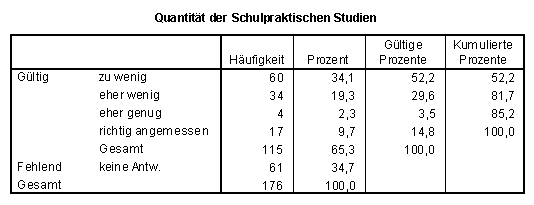
Der Wunsch der Referendare nach (viel) größerem Anteil fachdidaktischer Veranstaltungen in der 1. Ausbildungsphase ist sehr groß. Mehr als 90% wünschen offensichtlich eine starke Reduzierung des fachmathematischen Anteils, der (gemäß der z.Z. praktizierten Studienordnungen) bei 85% bis 90% liegen dürfte.
Von 11 Fachleitern sprechen sich 2 für ein Verhältnis 90 : 10 ( Mathematik : Mathe.Didaktik ) aus, 2 für ein Verhältnis 80 : 20 und 7 wünschen mindestens 30% Anteil fachdidaktischer Veranstaltungen.
Kommentare der Fachleiter:
* Es sollte sich um fachdidaktische Inhalte handeln, die nicht
der Unterrichtsüberprüfung bedürfen.
* Es kommt wesentlich auf die Qualität der fachdidaktischen Inhalte an; Schulnähe ist oft nicht gewährleistet.
* Gewußt "was" ist (mindestens) so wichtig wie gewußt "wie".
* Ich habe wenig hilfreiche fachdidaktische Veranstaltungen erlebt. Zu flach!
SPSS-Tabelle zu Frage 3.5:
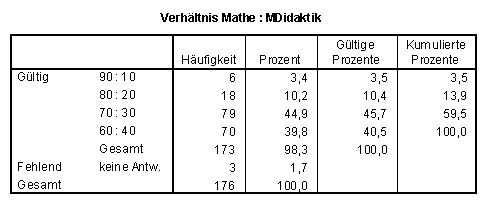
Nachfolgende SPSS-Kreuztabelle zeigt:
Obwohl (oder gerade weil?) sie die Qualität der fachdidaktischen Veranstaltungen kritisieren, wünschen sich viele Lehramtskandidaten viel mehr und bessere mathematikdidaktische Veranstaltungen zur Vorbereitung auf das Berufsfeld des Mathematiklehrers in der Sek. II / I.

Der derzeitige Anteil der Erziehungswissenschaftlichen Studien von 20% wird sehr unterschiedlich eingeschätzt (vgl. Frage 3.6). 44% halten den Anteil für "(eher) zu hoch". 41% halten ihn für "(eher) zu niedrig".
Von den Fachleitern sagen 7, der Anteil der Erziehungswissenschaften sei "(eher) zu hoch", 3 nennen ihn "eher zu niedrig" und einer sagt, er sei "o.k.". Kommentare der Fachleiter:
* "Die Inhalte in EW sollten mehr Relevanz für Unterricht haben."
* "...kaum Effizienz für das spätere Berufsleben."
* "Es liegt keine Praxiskopplung vor."
* "Wenn, wie in Köln der fachdidaktische Schein durch einen "Mathematik"-schein ersetzt werden kann und meine Referendare derzeit keine Ahnung von allgemeiner – oder gar Fachdidaktik haben, muß der Anteil zu gering sein."
SPSS-Tabelle zu Frage 3.6:
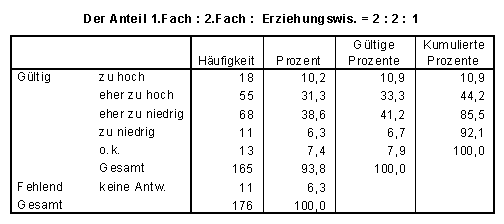
Von den 88%, die schlechte Erfahrungen in den Erziehungswissenschaften gemacht haben, wünschen fast gleich viele hier einen größeren Anteil bzw. einen geringeren Anteil. Der Sinn dieses Studienbereiches für das Berufsfeld Mathematiklehrer in der Sek II / I scheint sehr unklar. Hier besteht Handlungsbedarf für die Prüfungs- und Studienordnung!
SPSS-Kreuztabelle zu Frage 3.6 und 3.7:
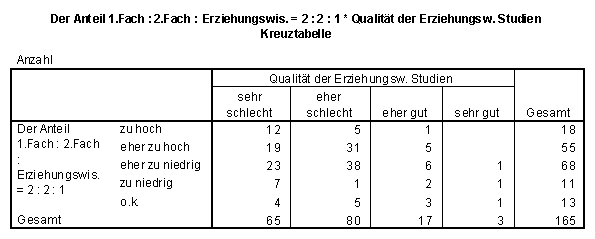
Ein vorrangiges Ziel der 1. Ausbildungsphase ist mathematische Kompetenz und Selbstvertrauen im Hinblick auf die Tätigkeit als Mathematiklehrer.
Die Korrelation zwischen Selbstvertrauen und
mathematischer Kompetenz ist signifikant:
Das Bewußtsein ("Gefühl"), mathematisch gut gerüstet
zu sein, stärkt das Selbstvertrauen im Hinblick auf die eigene Tätigkeit
als Mathematiklehrer.
SPSS-Kreuztabelle zu Frage 4.1: mathematische Kompetenz * Selbstvertrauen
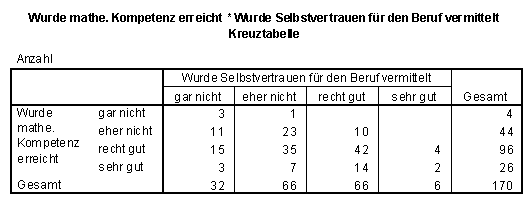
Ein Zusammenhang zwischen Selbstvertrauen und Bewertung der Anforderungen im Grundstudium ist ebenso wenig nachweisbar wie mit der Bewertung des Hauptstudiums und der "selbständig aktiven Bearbeitung von unterrichtspraktischen Problemen".
SPSS-Kreuztabelle zu Frage 1.3 * 4.1: Anforderungen im Grundstudium * Selbstvertrauen

SPSS-Kreuztabelle zu Frage 3.3 * 4.1: selbständige aktiv Probleme bearbeitet * Selbstvertrauen

Eine ("schwächere") Korrelation besteht jedoch zwischen der sich selbst zugeschriebenen mathematischen Kompetenz und der Bewertung der Anforderungen im Hauptstudium – nicht jedoch im Grundstudium.
SPSS-Kreuztabelle zu Frage 2.3 * 4.1: Anforderungen im Hauptstudium * Selbstvertrauen

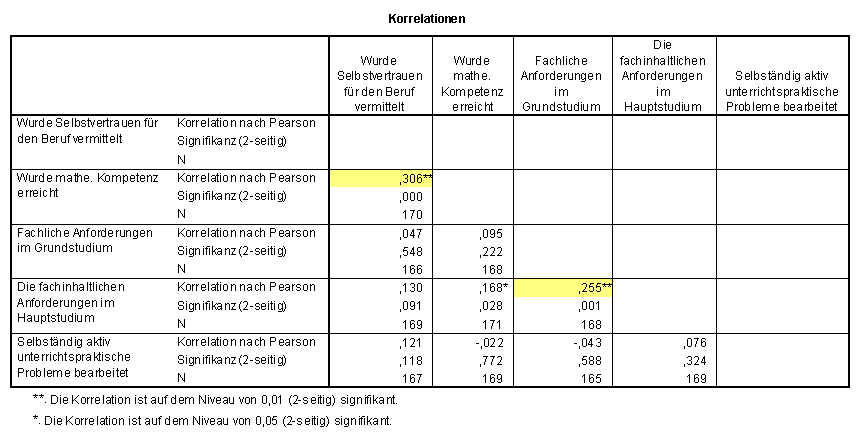
In Frage 4.2 wurde gefragt "welche Teilgebiete sollten im Studium... angeboten werden?"
Da Infinitesimalrechnung und Lineare Algebra zum Pflichtkanon des Grundstudiums gehöhren, wurden diese Gebiete nicht aufgeführt.
Von mehr als 50% der Referendarinnen und Referendare wurden Wahrscheinlichkeitsrechnung, Analytische Geometrie, Logik/Grundlagen, Algebra und Zahlentheorie genannt.
Die Bewertungen der Fachleiter stimmen weitgehend mit diesen überein. Beachtet werden sollte jedoch eine höhere Bewertung der Algebra bei den erfahrenen Fachleitern.
| a) Mathematische Teilgebiete | Anzahl | Prozent (%) | # ...von
den 12 Fachleitern |
| Wahrscheinlichkeitsrechnung | 158 | 90 | 12 |
| Analytische Geometrie | 136 | 77 | 12 |
| Logik / Grundlagen | 101 | 57 | 8 |
| Algebra | 101 | 57 | 10 |
| Zahlentheorie | 98 | 56 | 7 |
| Funktionentheorie | 77 | 44 | 6 |
| Numerische Mathematik | 68 | 39 | 8 |
| Axiomatische Geometrie | 68 | 39 | 3 |
| Diff. Geometrie | 38 | 22 | 3 |
| Topologie | 14 | 8 | 2 |
| Maßtheorie | 12 | 7 | 2 |
Mit großer Mehrheit wünschen sich Lehramtskandidaten Veranstaltungen zur
Didaktik der... Analysis, Stochastik, Linearen Algebra und Geometrie für die Sekundarstufe II.
Der Wunsch nach stoffinhaltlich orientierten Veranstaltungen zur Geometrie , Algebra und Stochastik für die Sekundarstufe I ist unübersehbar.
Auch hier stimmen die Ansichten der Fachleiter mit denen der Referendare überein.
| b) Didaktik der... | Anzahl | Prozent (%) | # ...von
den 12 Fachleitern |
| Analysis | 168 | 96 | 11 |
| Stochastik | 153 | 87 | 10 |
| Linearen Algebra | 137 | 78 | 8 |
| Geometrie | 134 | 76 | 7 |
| Geometrie der Sek I | 125 | 71 | 7 |
| Algebra der Sek I | 108 | 61 | 8 |
| Stochastik der Sek I | 102 | 58 | 6 |
| Arithmetik der Sek I | 66 | 38 | 5 |
| Numerik | 49 | 28 | 4 |
Mehr als 50% der Referendare wünschen sich im Studium die Behandlung von methodischen Problemen (86%) des Mathematikunterrichts und Motivationsprobleme (78%). Für Fachpraktika in der Schule stimmten 73%, Geschichte der Mathematik wünschten 55%.
Auch hier stimmen Fachleiter und Referendare weitgehend überein. Beachtet werden sollte jedoch der höhere Stellenwert der Geschichte der Mathematik bei den Fachleitern.
| c) Didaktische Problemfelder | Anzahl | Prozent (%) | # ...von
den 12 Fachleitern |
| Methodische Probleme | 151 | 86 | 9 |
| Motivationsprobleme | 137 | 78 | 6 |
| Fachpraktika in der Schule | 129 | 73 | 9 |
| Geschichte der Mathe. | 96 | 55 | 11 |
| Lernpsychologische Fragen / Kognitionstheorie | 85 | 48 | 9 |
| Theorie der Lehr- und Lernprozesse | 67 | 38 | 8 |
| Empirische Unterrichtsforschung | 37 | 21 | 3 |
ANHANG:
Fragebögen – mit Prozentangaben für gegebene Antworten:
Befragung von Mathematikerinnen und Mathematikern
in Studienseminaren für die Sek II
Uns interessiert Ihre Meinung zur 1. Phase der Lehramtsausbildung für die Sekundarstufe II.
Ihre Mithilfe bei dieser Befragung kann zu einer Optimierung des LA-Studiums Sek II beitragen.
Wir danken Ihnen für Ihre Mithilfe.
Prof. Dr. P. Bungartz und Prof. Dr. A. Wynands Bonn, SS 1998
Ihr Alter: Durchschnittl. ca. 28_Jahre Geschlecht: m 84 w 90
Bezirksseminar : Ort ___________________ Beginn des Referendariats Monat/Jahr _____ / ____
Wo haben Sie ihr Erstes Staatsexamen bestanden? Univ. ( GHS) in ______________________
Wann war das? ______________________
Was ist neben Mathematik ihr anderes Studienfach: 2. Fach ____________ ggfl. 3. Fach ___________
In welchem Studienfach haben Sie Ihre Hausarbeit geschrieben? __ca. 20% in Mathe._____
Hat das Thema der Hausarbeit Relevanz für Ihre Tätigkeit als Lehrer?
gar nicht 36% eher nicht 35% eher wohl 19% sehr wohl 10%
Welches Studien- / Unterrichtsfach "mögen Sie am liebsten" ? Mathematik ca. 50% 2. Fach
1. Zum Grundstudium
1.1 Wie beurteilen Sie die Qualität Ihres Grundstudiums als Basis für Ihre Ausbildung als Mathematiker(in) und Lehrer(in)? ... insgesamt als ...
sehr schlecht 10% eher schlecht 53% eher gut 33% sehr gut 4%
1.2 Ihr Grundstudium war für alle Mathematikstudenten gleich. Es wurde nicht nach Diplom- und Lehramtstudium differenziert. Das ist Ihrer Meinung nach
sehr schlecht 28% (recht) schlecht 41% (recht) gut 26% sehr gut 5%
1.3 Die fachinhaltlichen Anforderungen im Grundstudium Mathematik waren...
eher zu niedrig 1% eher zu hoch 51% zu hoch 21% richtig angemessen 28%
1.4 Die Übungsaufgaben zu den Vorlesungen in Mathematik waren in der Regel
eher zu leicht 0% eher zu schwer 58% zu schwer 27% richtig angemessen 15%
1.5 Sollten im Grundstudium zu den Pflichtveranstaltungen Klausuren geschrieben werden?
auf keinen Fall 7% gelegentlich 28% auf jeden Fall 42%
ja, wenn dadurch eine Zwischenprüfung entfallen kann 23%
2. Zum Hauptstudium
2.1 Wie beurteilen Sie die Qualität Ihres fachwissenschaftlichen Hauptstudiums für Ihre Ausbildung zum (zur) Mathematiklehrer(in) der Sek II? ... insgesamt als ...
sehr schlecht 31% eher schlecht 48% eher gut 18% sehr gut 2%
2.2 Wie wurde in Ihrem Hauptstudium das Berufsfeld des Lehrers berücksichtigt?
gar nicht 45% zu wenig 51% ausreichend 3% sehr gut 1%
2.3 Die fachinhaltlichen Anforderungen im Hauptstudium Mathematik waren...
eher zu niedrig 0% eher zu hoch 50% zu hoch 32% richtig angemessen 18%
2.4 Befürworten Sie im Hauptstudium spezielle fachinahltliche Veranstaltungen (Vorle. / Semi.) für Lehramtskandidaten (getrennt von den Diplomkandidaten)?
gar nicht 2% eher nein 4% eher ja 25% auf jeden Fall 70%
3. Zur Mathematikdidaktik und zum Erziehungswissenschaftlichen Studium
3.1 Haben Sie Veranstaltungen besucht zu
allgemeinen fachdidaktischen Problemen des Mathematikunterrichts? nein 35% ja 65%
zu stoffinhaltlichen Fragen der Sek II? nein 39% ja 61%
zu stoffinhaltlichen Fragen der Sek I? nein 46% ja 54%
3.2 Wie beurteilen Sie die Qualität der von Ihnen besuchten Veranstaltungen zur Mathematikdidaktik im Hinblick auf Ihre Berufsvorbereitung als Lehrer(in)? ...insgesamt als ...
sehr schlecht 40% eher schlecht 44% eher gut 16% sehr gut 1%
3.3 In welchem Maße haben Sie selbständig aktiv in den fachdidaktischen Veranstaltungen unterrichtspraktische Probleme bearbeitet?
zu wenig 60% eher wenig 30% eher häufig 9% sehr häufig 1%
3.4 Haben Sie in Mathematik an Schulpraktischen Studien (Fachdid. Praktikum) teilgenommen?
nein 30% ja 70% wenn ja: Wie beurteilen Sie diese?
insgesamt war das... zu wenig 52% eher wenig 30% eher genug 4% richtig angemessen 15%
die Qualität war... sehr schlecht 7% eher schlecht 30% eher gut 48% sehr gut 15%
3.5 Wie sollte für das LA Sek. II in Mathematik das Verhältnis von fachinhaltlichen zu fachdidaktischen Studienanteilen (die sich auf Math.Unterricht beziehen, ohne "allgemeine Erziehungswissenschaf") in der gesamten 1. Ausbildungsphase sein?
100 : 0 0% 90 : 10 4% 80 : 20 10% 70 : 30 46% 60 : 40 41%
3.6 Während Ihres Studium mußten Sie ( neben dem Studium von 2 Fächern) auch Erziehungswissenschaften (EW) im Verhältnis 1.Fach : 2.Fach : EW = 2 : 2 : 1 studieren.
Der Anteil der EW ist... zu hoch 11% eher zu hoch 33% eher zu niedrig 41% zu niedrig 7% o.k. 8%
3.7 Wie beurteilen Sie Ihre Erziehungswissenschaftlichen Studien im Hinblick auf Ihre Berufsvorbereitung als Lehrer(in)? ... insgesamt als ...
sehr schlecht 40% eher schlecht 48% eher gut 10% sehr gut 2%
4. Zum guten Schluß
4. 1 Ihr Mathematikstudium sollte Ihnen mathematische Kompetenz vermitteln. Wurde dieses Ziel erreicht?
gar nicht 2% eher nicht 26% recht gut 57% sehr gut 15%
Ihr Mathematikstudium sollte Ihnen Selbstvertauen für Ihren späteren Beruf vermitteln. Wurde dieses Ziel erreicht?
gar nicht 19% eher nicht 39% recht gut 39% sehr gut 4%
4.2 Welche Teilgebiete sollten im Studium zukünftiger Mathematiklehrer der Sek II (auf jeden Fall) angeboten werden? (ergänzen Sie ggfl. bitte die Liste!)
a) Stoffinhalte: Logik/Grundlagen 57% Analytische Geometrie 77%
Differentialgeometrie 22% Wahrscheinlichkeitsrechnung 90%
Algebra 57% Topologie 8% Zahlentheorie 56% Numerische Mathe. 39% Funktionentheorie 44% Maßtheorie 7% (axiomat.) Grundl. der Geometrie 39%
....................................................................... .............................
b) Didaktik der ..... Analysis 96% Li. Algebra 78% Numerik 28%
Stochastik 87% Geometrie 76% Arithmetik in der Sek I 38%
Algebra i.d. Sek I 61% Geometrie Sek I 71% Statistik/Wahrsch. Sek I 58%
.....................................................................................................
Themen der M.didaktik: methodische Probleme des MU 86% Theorien von Lehr-, Lern-Prozesse 38% Lern- und kognitionsspychologische Fragen 48% Motivationsprobleme 78%
Empirische Unterrichtsforschung 21% Fachpraktika in der Schule 73%
........................................ ...............................................................
c) Geschichte der Mathematik 55%
Fragen an die Fachleiter für Mathematik
Dürfen wir auch Sie als Fachleiter(in) für
Mathematik noch um Beantwortung folgender Fragen bitten?
Wann haben Sie Ihr 1. Staatexamen bestanden? 19__ Wo war das? _________________
Was ist neben Mathematik Ihr 2. Fach? _______________ 3. Fach? ____________________
Hatte das Thema Ihrer Hausarbeit im 1.
Staatsexamen Relevanz für Ihre Tätigkeit als Lehrer? ja___ nein___
(Kommentar:)_____________________________________________________________________________
1. Die Erste Staatsarbeit
sollte grundsätzlich eine fachwissenschaftliche Arbeit sein , Ja__ Nein__
kann sowohl fachinhaltliche als auch fachdidaktische Schwerpunkte haben. Ja__ Nein__
(Kommentar:)_______________________________________________________________________
2. Das Grundstudium sollte in Mathematik für Lehramtskandidaten und Diplomstudenten
gemeinsam organisiert sein. Ja__ Nein__
(Kommentar:)_______________________________________________________________________
3. Im Hauptstudium sollte das Berufsfeld des Mathematiklehrers
nicht__ gelegentlich__ häufig__ sehr stark__
berücksichtigt werden.
(Kommentar:)_______________________________________________________________________
4. Wie wichtig ist Ihrer Meinung nach eine eigene Unterrichtspraktische Erfahrung der Lehramtskanditaten während der 1. Ausbildungsphase an der Universität?
sehr wichtig__ wichtig__ weniger wichtig__ nicht wichtig__
(Kommentar:)_______________________________________________________________________
5. Wie sollte für das LA Sek. II in Mathematik das Verhältnis von fachinhaltlichen zu fachdidaktischen Studienanteilen (die sich auf Math.Unterricht beziehen, ohne "allgemeine Erziehungswissenschaf") in der gesamten 1. Ausbildungsphase sein?
100 : 0 90 : 10 80 : 20 70 : 30 60 : 40
(Kommentar:)_______________________________________________________________________
6. Während des Studiums müssen LA-Kandidaten ( neben dem Studium von 2 Fächern) auch Erziehungswissenschaften (EW) im Verhältnis 1.Fach : 2.Fach : EW = 2 : 2 : 1 studieren.
Ist der Anteil der EW zu hoch eher zu hoch eher zu niedrig zu niedrig
(Kommentar:)_______________________________________________________________________
7. Welche Teilgebiete sollten im Studium zukünftiger Mathematiklehrer der Sek II (auf jeden Fall) angeboten werden? (ergänzen Sie ggfl. bitte die Liste!)
a) Stoffinhalte: Logik/Grundlagen Analytische Geometrie
Differentialgeometrie Wahrscheinlichkeitsrechnung
Algebra Topologie Zahlentheorie Numerische Mathe. Funktionentheorie Maßtheorie (axiomat.) Grundlagen der Geometrie
....................................................................... .............................
b) Didaktik der ..... Analysis Li. Algebra Numerik
Stochastik Geometrie Arithmetik in der Sek I
Algebra in der Sek I Geometrie i d Sek I Statistik/Wahrschein. i d Sek I
.....................................................................................................
Themen der M.didaktik: methodische Probleme des MU Theorien von Lehr-, Lern-Prozesse Lern- und kognitionsspychologische Fragen Motivationsprobleme
Empirische Unterrichtsforschung Fachpraktika in der Schule
........................................ ...............................................................
c) Geschichte der Mathematik
In den Bericht sind an entsprechender Stelle die Antworten der Seminarfachleiter eingearbeitet.
Antworten der Seminar_Fachlehrer(innen) – Fachleiter von Sem.Nr. 1, 2, 10, 12, 14 antworteten nicht.
S-Nr. |
3.1 | 3.2 | 4 | 5 | 6 | 7 | 8 | 9 | 11 | 13 | 15 | 16 | |
Examen |
91 | 74 | 71 | 70 | 69 | 64 | 76 | 91 | 73 | 81 | 81 | 67 | |
in |
Oberhausen | Emmerich | Bonn | Bochum | Köln | Münster | Darmstadt | Münster | Münster | Bielefeld | Bonn | Bonn | |
2.Fach |
Ph | Phil. | Ph | Infor. | Geogr. | Physik | SoWi | Physik | - | Physik | Physik | Physik | |
3.Fach |
Infor. | Sport | Metallg | ||||||||||
HA-MU |
2 | 1 | 2 | 2 | 2 | 2 | 1 | 2 | 2 | 2 | 2 | 2 | |
1a |
2 | 2 | - | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 1 | |
1b |
1 | 1 | 1 | 2 | - | - | 1 | 1 | 1 | 1 | 1 | 2 | |
2 |
1 | - | 1 | 2 | 1 | 2 | 2 | 1 | 1 | 1 | 1 | 1 | |
3 |
3 | 3 | 3 | 3 | 3 | 4 | 4 | 3 | 4 | 3 | 4 | 2 | |
4 |
2 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | 3 | 2 | 2 | 1 | |
5 |
4 | 2 | 4 | 4 | 4 | 2 | 4 | 5 | 5 | - | 3 | 3 | |
6 |
3 | 2 | o.k. | - | 2 | 1 | 3 | 2 | 2 | 2 | 3 | 2 | |
Logik |
1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||||
AnGeo |
1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
DifGeo |
1 | 1 | 1 | ||||||||||
Wahr |
1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
Alge |
1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||
Top |
1 | 1 | 1 | ||||||||||
Zahl |
1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||
NuMa |
1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||||
Futhe |
1 | 1 | 1 | 1 | 1 | 1 | |||||||
Maß |
1 | 1 | |||||||||||
Gr.Geo |
1 | 1 | 1 | ||||||||||
Didaktik |
|||||||||||||
Anal |
1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||
LiAl |
1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||||
Num |
1 | 1 | 1 | 1 | |||||||||
Stoch |
1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||
Geo |
1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||
Sek I |
1 | ||||||||||||
Arith |
1 | 1 | 1 | 1 | 1 | ||||||||
Alge |
1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||||
Geo |
1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||
Stat |
1 | 1 | 1 | 1 | 1 | 1 | |||||||
Did.The |
|||||||||||||
Meth |
1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||
Theor |
1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||||
kognit |
1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||
Motiv |
1 | 1 | 1 | 1 | 1 | 1 | |||||||
Empir |
1 | 1 | 1 | ||||||||||
Prakt |
1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||
Geschi |
1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||
Kommentare der Fachleiter
| von Sem. Nr. | zu | |
| 3.1 | HA | leider (keine Relevanz) |
| 2 | Gemeinsam besuchte Grundvorlesungen schließen unterschied. Akzentuierung (3., 4. Sem.) nicht aus. | |
| 4 | Umsteigen ist hier leichter möglich | |
| 3.2 | HA | Es kann mehr in den Unterricht als man gemeinhin denkt |
| 2 | Es ist gut, wenn schon der "Grundstudent" Einblick in seinen späteren Beruf erhält. | |
| 4 | HA | Meromorphe Funktionen sind schulisch nicht gebrauchbar |
| 1 | Innovationen im Schulbereich könnten so eher gefördert werden | |
| 2 | Dies "ja" gilt speziell für Lehramtskandidaten, die in Sek II unterrichten werden! | |
| 3 | Hier gilt es, eklatante Lücken zu schließen! | |
| 4 | Schulpraktische Studien geben den Studenten erste Rückmeldungen zur passenden (Unpassenden) Berufswahl! | |
| 5 | Dies Verhältnis sollte auch in die 1. Staatsprüfung ausstrahlen! | |
| 6 | (das angegb. Verhätnis 2:2:1 hält der Befragte für) eher passend! | |
| 7a | jeweils Grundlagen! (in allen angegeb. Gebieten) | |
| 7b | exemplarische Ansätze! (in allen angegeb. Gebieten) | |
| M.Did | speziell Theor. und kognit. Fragen in enger Anbindung an mathem. Fragestellungen | |
| 7c | als "Steinbruch" für genetische Ansätze! | |
| 5 | 6 | Die Inhalte in EW sollten mehr Relevanz für Unterricht haben |
| 7a | viele Gebiete ansprechen, aber nicht 3 Semester lang | |
| 7b | (Did. der Geometrie mit "!!" als besonders wichtig gekennzeichnet.) | |
| 7c | ganz wichtig. Problemstellung nicht von der Genese abschneiden. | |
| 6 | 6 | kaum Effizienz für das spätere Berufsleben |
| 7 | HA | Es war ein Gebiet aus der Homologischen Algebra, das absolut keine Beziehung zur Lehrtätigkeit hatte. |
| 2 | Die Inhalte für die Schule bilden einen eigenst. Bereich. | |
| 3 | Dies sollte hauptsächlich im fachwissenschaftlich. Bereich stattfinden. | |
| 4 | um die Berufstauglichkeit ermessen zu können. | |
| 5 | Es sollte sich um fachdidaktische Inhalte handeln, die nicht der Unterrichtsüberprüfung bedürfen. | |
| 6 | Es liegt keine Praxiskopplung vor. | |
| 7b | s. 5! ( hier sind keine Stoffinhalte angekreuzt; ist gemeint: diese /alle sind statt der Erziehungswissenschaften zu berücksichtigen!?) | |
| 8 | HA | Thema: "Anpassung des Lehrers" (Praxisschock) |
| 1 | Fachdidaktik weiter gefaßt --> Rolle des Lehrenden | |
| 2 | zeitlich Diplom --> wo ist Zeit für Didaktik? | |
| 3 | Anwendungsbezüge herstellen | |
| 4 | ungeeignete können den Studiengang wechseln | |
| 6 | Wenn, wie in Köln, der fachdidaktische Schein durch einen "Mathematik"schein ersetzt werden kann und meine Ref. derzeit keine Ahnung von allgemeiner - oder gar Fachdididaktik haben, muß der Anteil zu gering sein! | |
| 7c | auf jeden Fall! | |
| 9 | HA | Aber Auseinandersetzung mit didaktischen Gesichtspunkten, da das Experiment (Physik) für Wahlfachpraktikum von Diplomstudenten entwickelt wurde. |
| 2 | Es müssen auch Studiengangsspezifische Vorlesungen angeboten werden. Gemeinsame Organisation um ggf. einen Wechsel zu ermöglichen. | |
| 4 | Sie sollte v.a. zu einem frühen Zeitpunkt des Studiums möglich sein, um eine evl. Nichteignung früh festzustellen. | |
| 5 | Es kommt wesentlich auf die Qualität der fachdidktischen Inhalte an, Schulnähe ist oft nicht gewährleistet. | |
| 6 | Vorrangige Kriterien: Qualität - Praxisbezug -nicht Qunatität | |
| 7 | Computereinsatz im Unterricht | |
| 11 | 2 | kann nicht schaden |
| 3 | Referendare haben keinen Überblick über die Inhalte der Schulmathematik | |
| 4 | wichtiger im Hauptstudium | |
| 5 | gewußt "was" ist (mindestens) so wichtig wie gewußt "wie" | |
| 6 | EW ist nur Theorie, die Praxis fehlt | |
| 7c | nicht so wichtig | |
| 13 | 5 | Ich habe weinig hilfreiche fachdid. Veranstaltungen erlebt. Zu flach! |
| 16 | 1 | Da beide Schwerpunkte wichtig sind und der 2. die Referendarzeit prägt, sollte der erste unbedingt im Rahmen des Fachlichen angemessen vertreten sein. |
| 4 | Wichtig scheint mir hier weniger der Ausbildungsaspekt als die Möglichkeit, die eigene grundsätzliche Eignung zu überprüfen. |