Zusammenfassung:

Die PISA-Klassifikation nach "Typen mathematischen Arbeitens" (technische Aufgaben, rechnerische und begriffliche Modellierungs- und Problemlöseaufgaben) wird konfrontiert mit einem der zentralen Bereiche der "entwickelnden" Mathematikdidaktik, der Schulbuchkonstruktion. Aufgaben in Schulbüchern und Tests sollen demnach ausgewogen über diese Typen streuen. Ausgewogenheit zu erreichen ist das Ziel eines "grundbildenden Mathematikunterrichts", dem auch PISA verpflichtet war.

PISA, das "Programme for International Student Assessment" (OECD 1999; Baumert & al. 2001, 2002,2003) hatte die Intention, Indikatoren zu gewinnen über den Stand der Bildung in 32 teilnehmenden Ländern. Dadurch sollte eine konstruktive Weiterentwicklung des Mathematikunterrichts angeregt werden. Allerdings war und ist PISA zunächst ein Leistungstest. Anregungen für den Unterricht können also nur von den Konzeptionen her kommen. Die PISA-Studie focussierte im fachinhaltlichen Teil auf Merkmale einer Grundbildung von Schülerinnen und Schülern in einer modernen, entwickelten Gesellschaft. Schlüssel dafür ist der Begriff "literacy" (OECD 1999). Im deutschen Ergänzungstest (Neubrand & al. 2001) wurde der Begriff "mathematical literacy" ausdifferenziert und erweitert zu einem auch in der deutschen Allgemeinbildungsdiskussion zu verankernden Begriff "mathematischer Grundbildung".

Versucht man diese allgemeinen Konzeptionen produktiv in den verschiedenen Aufgabenbereichen der Mathematikdidaktik zu verwenden, also nicht nur - wie bei PISA sozusagen "direkt" - als Forschungskonzepte sondern auch als Vorlage für entwicklungsbezogene Vorhaben einzusetzen, dann ist nach Konkretisierungen gefragt. PISA-Deutschland selbst (Klieme, Neubrand & Lüdtke 2001; Neubrand & al 2002, Neubrand 2002; Knoche & al. 2002) hat dafür Vorarbeiten geleistet, indem "mathematische Grundbildung" konkretisiert wird als ausgewogene Performanz in drei Typen mathematischen Arbeitens. Es ergaben sich diese Typen mathematischen Arbeitens aus grundsätzlichen Überlegungen zu charakteristischen Merkmalen der Mathematik (BLK 1997, Kap. 51), auf der Basis mathematik-didaktischer Verankerungen (Neubrand & al. 2001) und wegen des Anschlusses an die kognitionspsychologische Forschung (Hiebert 1986; Neubrand & al. 2001; J. Neubrand 2002):

• Technische Aufgaben,
• Rechnerische Modellierungs- und Problemlöseaufgaben,
• Begriffliche Modellierungs- und Problemlöseaufgaben.

"Technische Aufgaben" sind dabei diejenigen Aufgaben, bei denen ein vorgegebener Ansatz mittels bekannter mathematischer Prozeduren (Rechnen oder Konstruieren nach vorgegebenen Regeln) kalkülhaft durchzuführen ist. Die "rechnerischen Modellierungs- und Problemlöseaufgaben" sind Anwendungsaufgaben oder innermathematisch problemhaltige Aufgaben, bei denen die Mathematisierung bzw. das Erstellen eines Lösungsschemas auf einen Ansatz führt, der rechnerisch oder "prozedural" zu bearbeiten ist. Vor allem die "klassischen" Textaufgaben sind von dieser Art, denn meist läuft eine solche Aufgabe darauf hinaus, die gesuchte Größe aus einem Ansatz heraus zu berechnen.

Mit dem Ausdruck "begrifflich" sind Aufgaben bezeichnet, bei denen die Modellierung oder die Problemlösung mittels des Einsatzes begrifflichen Denkens durchgeführt werden kann, z.B. durch Herstellen begrifflicher Zusammenhänge, durch logisches Argumentieren oder durch Aufstellen einer Systematik. Essentiell für "begriffliches mathematisches Arbeiten" in diesem Sinne ist, dass ein Zusammenhang zwischen Wissenselementen hergestellt werden muss, wobei sich dieser Zusammenhang nicht erst nach Durchführen eines Algorithmus erschließt, sondern aufgrund einer erkannten oder erst konstruierten Beziehung zwischen den Gegenständen formuliert werden muss.

Alle drei Arten des Vorgehens sind charakteristisch für mathematisches Arbeiten. Dagegen ist die sonst oft in der Wissenspsychologie benutzte Konzept-Prozess-Dichotomie für die Mathematik weniger passend. Gerade die unterschiedlichen Prozesse - das Herstellen eines gedanklichen Zusammenhangs einerseits oder andererseits das Durchführen eines Algorithmus mit oder ohne Modellierung oder Ansatzfindung - sind es, welche die kognitive Spannweite mathematischen Arbeitens ausmachen. Ersteres wird von Hiebert (1986) als "conceptual knowledge" bezeichnet. Wenn besonders die zuletzt genannte Aktivität in einer Aufgabe erforderlich ist, sprechen wir von einer "begrifflichen Modellierungs- und Problemlöseaufgabe".

An der bei PISA benutzten Dreiteilung mathematischen Arbeitens, die ja zunächst aus Forschungszusammen-hängen kommt, kann man sich auch hinsichtlich der "Entwicklungs"-Dimension der Mathematikdidaktik orientieren. Ein zentrales Entwicklungsfeld für Fachdidaktik ist die Konzeption, Erstellung und schließlich auch die Bewertung von Schulbüchern. Beide Autoren dieses Aufsatzes waren in den letzten Jahren mit beidem befasst, einerseits mit Konzeption und Auswertung des PISA-Tests in Deutschland (Neubrand & al. 2001; Knoche & al. 2002), andererseits mit einer Neubearbeitung des Unterrichtswerks Welt der Zahl (WdZ, 2001) für die Hauptschule, und zwar AW als Herausgeber und Autor, MN als Berater bei den Teilen des Buches, die besonders eng mit "mathematischer Grundbildung" verbunden sind.

Speziell zu diesem Zweck wurden den Kapiteln des Schulbuchs Welt der Zahl sogenannte "Durchblick"-Seiten angefügt. Diese sollen Aufgaben enthalten, die nicht nur den Stoff des aktuellen Kapitels repetieren, sondern kumulatives und vernetzendes Lernen fördern und auch länger zurückliegende Stoffe in neuen Zusammenhängen wieder aufnehmen. Die "Durchblick"-Seiten dienen daher

• der Wiederholung wichtiger Basiskenntnisse und Fertigkeiten aus zurückliegenden Kapiteln und Gebieten,
• der Vernetzung von Fähigkeiten aus verschiedenen Stoffgebieten in innermathematischen Anwendungen oder in authentischen oder realitätsnahen außermathematischen Situationen,
• der Strukturierung von Situationen mit mathematischen Begriffen, der Reflexion über (Lösungs-) Wege, der Verallgemeinerung und Begründung von Aussagen und Ergebnissen.

Die Überlegungen zur PISA-Konzeption zeigen, dass es notwendig und möglich ist, beim "Durchblick" auf ein breites Verständnis mathematischen Arbeiten zu achten, und dass mit der obigen Klasseneinteilung ein Orientierungsmuster für die Sicherung dieser Breite zur Verfügung steht. Die Herstellung einer solchen Breite der mathematischen Kenntnisse ist gerade in der Hauptschule ein spezifisches Problem. Bereits in der Expertise zum BLK-Modellversuche SINUS (BLK 1997), und wieder im nationalen PISA-Framework (Neubrand & al. 2001) wurde darauf hingewiesen, dass es nicht sinnvoll ist, den Mathematikunterricht der Hauptschule aus vermeintlich realistischen Umsetzungsüberlegungen heraus nur auf Teile der "Spannweite mathematischen Wissens" zu beschränken. Dies ist prinzipiell keine Frage, die man auf der Schulformebene abhandeln kann. Fundamentale Begriffe der Mathematik -z.B. Funktion oder Variable als Beschreibungsmerkmal für Prozesse vielfältiger Art, die Spielarten von "Mustern" usw.- müssen auch in der Hauptschule zur Geltung kommen. Freilich ist die äußere Form dieser Begriffe, nicht aber deren Vorkommen überhaupt, abhängig von der jeweiligen Schülerschaft und deren Fähigkeitsspektrum.

PISA hat mit seinem Aufgabenmaterial gezeigt, dass rechnerisches Modellieren und begriffliches Arbeiten auf allen Schwierigkeitsstufen möglich ist, und dass es für alle Leistungsgruppen kognitiv anspruchsvolle und dennoch nicht notwendig auch technisch aufwändige mathematische Aufgaben gibt. Besonders deutlich wird dies in der Auffächerung der Aufgaben sowohl nach der Schwierigkeits- als auch nach der Fähigkeitsdimension, wie sie z.B. bei Neubrand & al. (2002) vorgenommen wurde. Inhaltlich gesehen zeigen dabei die internationalen PISA-Aufgaben (OECD 2002) in Anknüpfung an Freudenthals Konzepte (Freudenthal 1977) - wie der Anwendungsbezug zur strukturellen und begrifflichen Vertiefung führen kann. Die nationalen Ergänzungsaufgaben (Klieme & al. 2001; Knoche & al 2002) verweisen mit der gegenüber dem internationalen PISA-Framework erweiterten Sichtweise auf mathematische Grundbildung darauf, dass auch innermathematische Kontexte (nicht: "Techniken"!) als gleichrangig anzusehen sind.

Diese Konzeption mathematischer Grundbildung ist also einer "Komplementarität von Anwendungsorientierung und Strukturorientierung" verpflichtet, wie sie Heinrich Winter immer wieder forderte (z.B. Winter 1995 mit Bezug zur "mathematische Grundbildung"): Anwendungsbezogenes Arbeiten allein, nur motiviert durch die vordergründige Brauchbarkeit, vertieft mathematisches Wissen nicht ins Allgemeine hinein. Und genau das "ist" Mathematik. Und umgekehrt bleiben mathematische Strukturen ohne Bindung zu Anwendungen, Bildern, Kontexten etc. "leer".

Neues Wissen und Können soll nicht nur additiv vorher erworbenem hinzugefügt werden. Es muss zusammen-passen und vernetzt werden mit bekannten Begriffen, Anwendungsmöglichkeiten und Methoden. Ziele sind das Herstellen "vertikalen Lerntransfers", systematisches Lernen innerhalb der Mathematik und "horizontaler Lerntransfer", also flexible Anwendungsfähigkeit und "lateraler Lerntransfer", d.h. Erwerb von Methoden und selbstständiges Weiterlernen ( Zitate aus Weinert 2001). Neue Begriffe und Methoden müssen alte ergänzen oder erweitern, wenn diese alten zur Beantwortung neuer Fragen nicht mehr ausreichen.

Somit sind die folgenden Kennzeichen Konkretisierungen für kumulatives und vernetzendes Lernen:

• Wiederholen der Kenntnissen aus früher behandelten Lernabschnitten.
• Aufgaben, die Fertigkeiten in verschiedenen Stoffgebieten aus der Arithmetik und Geometrie erfordern, wachhalten und miteinander in Beziehung setzen. Beispiele:
  - Veranschaulichen und graphisches Darstellungen von Zahlen,
  - Arbeiten mit Größen; Daten sammeln, ordnen, interpretieren, darstellen.
• Arbeitsaufträge, die arithmetisches und geometrisches Denken und Arbeiten ansprechen.
  - Figuren, Muster strukturieren, variieren und ihre Maße bestimmen,
  - Skizzieren, konstruieren und berechnen von Körpern.
• Methodenvernetzendes Lernen wird dadurch gefördert, dass ein Wechsel der Darstellung für die Aufgabenstellung oder bei ihrer Lösung gefordert wird. Beispiele:
  - Wechsel zwischen Text, Skizze, Notation eines Rechenwegs und
  - zu Bildern, Skizzen oder Texten eine mathematische Aufgabenformulierung notieren und lösen.
• Flexibles Arbeiten und Vernetzung von Methoden fördern besonders solche Aufgaben, die für verschiedene Lösungswege offen sind. Dazu sollte ein Problem so präsentiert werden, dass die Aufgabenstellung und die zur Lösung notwendigen Angaben - wenigstens zum Teil - gefunden werden können, zum Beispiel in authentischen Quellen wie Zeitung oder Lexikon, in einer Graphik, einer Illustration oder in einem Foto zu einer realen Situation. Wie die Lösung gefunden wird - durch zielgerichtetes Probieren oder Rechnen mit konkreten Zahlenwerten, durch zeichnerische Konstruktion, oder z.B. durch begriffliches Begründen - bleibt dem Lösenden überlassen. Aufgaben können auch dadurch geöffnet werden, dass Vorgabedaten zum Teil oder ganz fehlen oder die Fragestellung offen bleibt. Problematisch ist, wie "offen" eine von Lernenden zu bearbeitende Aufgabenstellung sein kann. In Abhängigkeit vom Adressaten ist zu entscheiden, wann z.B. Fragen, Daten oder Lösungswege fehlen können und die Lernenden mit Aussicht auf Erfolg aufgefordert werden, Fragen selber zu stellen und diese dann mit selbstgewählten Methoden zu bearbeiten.

Neben "kleinen" Aufgaben zum Üben spezieller Basiskompetenzen -z.B. Kopfrechnen mit einziffrigen Zahlen und Zehnerpotenzen, Überschlagsrechnen, Maßumwandlungen - sollten häufig(er) komplexe Aufgaben im Mathematikunterricht Beachtung finden. Gerade diese Aufgaben sind in besonderem Maße geeignet, vernetztes Denken auszubilden. Bei allen guten Ideen und Wünschen sollte aber besonders in der Hauptschule keine Überforderung der Schülerinnen und Schüler erfolgen; Frust und kontraproduktive Ängste wären absehbare Folgen. Deutlich gesagt sei aber, dass sich die hier angegebenen Beispiele nicht nur an die ca. 30% leistungsstarken Schülerinnen und Schüler in der Hauptschule richten, deren mathematische Fähigkeiten derjenigen in der Realschule oder im Gymnasium entspricht. Manche Schülerinnen und Schüler werden gerade durch herausfordernde Aufgaben gefördert.

Die Beispiele sind hier eingeordnet nach Jahrgangsstufe und Aufgabenklasse oder Typ. Alle Aufgaben sind dem Unterrichtswerk "Welt der Zahl - Hauptschule NRW" (Wynands 2001) entnommen. Die intendierten Lernziele erfüllen die Anforderungen des derzeit gültigen Lehrplans in NRW. Die meisten Aufgaben zum Modellieren und Problemlösen können durchaus am Anfang einer Lernsequenz stehen, wenn man problemorientiert in ein neues Stoffgebiet einsteigen will. Am Ende einer Unterrichtssequenz haben sie ihren Platz, um neu gelernte mit länger bekannten Begriffen und Methoden zu vernetzen und zu festigen.

Technische Fertigkeiten sind unzweifelhaft "Grundlage" für Modellierungs- und Problemlöseprozesse. Freilich darf "Grundlage" nicht heißen, dass diese Fertigkeiten im Lernprozess immer "zuerst" entwickelt werden müssten. Wiederholungen aus zurückliegenden Kapiteln und Gebieten sind sehr wichtig. Sie können durchaus auch mit dieser Funktion benannt werden. Aber anders als in Leistungstests, bei denen man die Typen mathematischen Arbeitens auch z.B. zu Analysezwecken isolieren kann, sind im Lernprozess bereits hier vielfältige Verknüpfungen vorzusehen. Die Methoden hierfür sind bekannt: Operative Vernetzungen, Vernetzungen über Stoffgebiete hinweg, Verbindungen von Faktenwissen und technischen Fertigkeiten sowie Anregungen zu Begriffsbildungen, die mit der Entwicklung technischer Fertigkeiten parallel laufen können. Daher sind auch "freiere" Formate für diese Fragestellungen möglich.

Zum Wachhalten technischer Fertigkeiten seien hier nur wenige Beispiele für die Jahrgangsstufen 5/6 genannt, die sich auf Terme und "Größen" beziehen. Für die anderen Jahrgangsstufen können entsprechende konstruiert werden. Man beachte hierzu auch die Test-Aufgaben am Ende dieses Beitrages.

1. 4+2× 3 (4+2)× 3 4× (2+3) 4: (2-1) 4:2 - 1 4-2× 0 (4+2:1)× 0
2. Welche Zahlen haben genau 2 Teiler? Beachte: 1 teilt jede Zahl! Welche Zahlen sind Quadratzahlen?
   4 7 11 49 50 51 100 101 999 1000 1001 1 Million
3. Welche Größenangaben gehören zu Längen, welche zu Flächen? Sortiere und ordne.
   0,6 m 0,1 m² 50 mm 80 cm² 10 cm² 1 dm² 1/2 km 66 cm
   Welche konkreten Gegenstände sind so groß? Gib Beispiele hierzu an.
4. Arbeite mit diesen Längen: 305m, 905m, 195m, 95m, 550m, 650m, 450m, 915m, 805m, 85m.
   a) Sortiere. Beginne mit der kleinsten Länge. Berechne den größten Unterschied.
   b) Zwei passende Längen sollen zusammen 1 km ergeben. Schreibe alle auf.
   c) Wie viele gleich große Längen sind genau so lang wie alle hier angegebenen zusammen?

Rechnerische Modellierungs- und Problemlöseaufgaben sollen nach Möglichkeit nicht einfach "eingekleidete" Rechenaufgaben sein. Vernetzung von verschiedenen Stoffgebieten und Rechnen "quer" zur ursprünglichen Art und Zielsetzung des Gelernten sind intendiert. Dabei wird Flexibilität im Umgang mit den mathematischen Inhalten in Anwendungssituationen erwartet. Rechnerische Modellierungs- und Problemlöseaufgaben können und sollen sich auf außermathematische oder auf innermathematische Kontexte beziehen.

Beispiele

1. Zeichne mindestens zwei Rechtecke mit einem Umfang von 20cm (einem Flächeninhalt von 36cm²). Schreibe die Maße für Länge und Breite daran. Bestimme den Flächeninhalt (Umfang). Färbe in deinen Rechtecken 1 Viertel rot, 1 Achtel blau. Welcher Anteil bleibt ungefärbt?
2. Wie oft schlägt dein Herz etwa in einer Minute? Wie oft an einem Tag? Schlägt es häufiger als 100 Millionen mal im Jahr? Wird dein Herz mehr als 10 Milliarden mal schlagen?
   
3. Leon denkt sich einen Sparplan aus: "Am 1. Tag spare ich 1 Cent, an jedem weiteren Tag doppelt so viel wie am vorhergehenden Tag."
   a) Wie viel Cent spart Leon am 4. Tag? Wie hoch ist die angesparte Summe nach 4 Tagen?
   b) Wie viel Euro muss Leon am 10. Tag (am 20. Tag) sparen, wenn er seinen Sparplan einhält?
   c) Nach wie vielen Tagen ist Leon Euro-Millionär? Schätze zuerst, dann rechne.
4. Mit vielen kleinen Würfeln der Kantenlänge 1 cm kannst du einen größeren Würfel bauen.
   a) Wie viele kleine Würfel brauchst du für den nächst größeren Würfel? Welche Oberfläche hat dieser? Wie weit sind die Ecken des kleinen, wie weit die des größeren Würfels von einander entfernt?
   b) Zeichne für Würfel die Zuordnung Kantenlänge
à Länge aller Kanten (Oberfläche, Volumen, Raumdiagonale) in ein Koordinatensystem. Ist die Zuordnung "proportional"? Begründe.
Anmerkung: Rechnen, Kopfgeometrie und Funktionsbegriff werden innerhalb eines gleichbleibenden Kontexts aktiviert.
5. Ein Hase hüpft von Hasenstadt nach Burghausen. Dabei verdoppelt er von Sprung zu Sprung seine Sprungweite. Sein erster Sprung ist 1 m weit. Burghausen ist 16 km von Hasenstadt entfernt.
   Anmerkung: Die Frage nach der Anzahl der Sprünge kann fehlen. Beispiele für weitere Fragen: Welche Annahmen machst du bei deinen Rechnungen und Antworten. Beim wie vielten Sprung ist die Sprungweite mindestens 100 km und wie weit ist der Hase dann?

Begriffliche Modellierungs- und Problemlöseaufgaben betreffen das Strukturieren, Begründen, Verallgemeinern. Eine wichtige Funktion haben sie für das kumulatives Lernen, indem sie vertikalen Transfer anregen. Allerdings sollte diese Funktion auch in den anderen Aufgabenklassen zum Ausdruck kommen. Begriffliche Modellierungs- und Problemlöseaufgaben beziehen sich ebenfalls in gleicher Weise auf außer- wie auf innermathematische Kontexte.

Beispiel

1. Eine große Tafel Schokolade wiegt 100g und kostet 90 Cent, eine kleine wiegt 40g und kostet halb so viel wie die große. Bei welcher Tafel bekommt man mehr für sein Geld? Kannst Du es "ohne Rechnen" entscheiden?
2. Du besitzt doch ein Geodreieck?! Wähle eine Kante als Drehachse. Drehe dein Geodreieck um diese Kante.
   a) Welche Drehkörper können entstehen? Skizziere die Drehkörper und schreibe Maße an deine Skizze.
   b) Was kannst du für die Drehkörper berechnen? Schreibe auf, was du wissen musst und wie du rechnest.
   c) Wie ändert sich das Volumen der Drehkörper, wenn du statt deines Geodreiecks das Schul-Geodreieck nimmst? (Schul-Geodreiecke sind häufig Vergrößerungen deines Geodreiecks im Maßstab 3,75 : 1 ).
3. Prüfe die Gleichungen. Sie sind der Anfang einer Serie. Setze die Serie um zwei weitere Gleichungen fort. Prüfe auch diese Gleichungen.
   (1+2)² = 1³ +2³ (1+2+3)² = 1³ +2³ +3³ (1+2+3+4)² = 1³ +2³+3³+4³.
   Anmerkung: Hier eröffnen sich viele weitere Fragen mit zunehmender Tiefe, z.B.:
   * Wie kann man linke und rechte Seite der Gleichungen geometrisch darstellen?
   * Welchen Wert hat die Summe der Kubikzahlen von 1 bis 10 (bis 100, bis n)?
   * Wie wächst das Quadrat von 1+2+3+4+... ? Kann das Quadrat der Summe 1 Million sein?
   * Stelle ähnliche Fragen bei dieser Serie:
   1=1, 4-1 = 1+2, 9-4+1 = 1+2+3, 16-9+4-1 = 1+2+3+4 .....

Ausgewogenheit über die Typen mathematischen Arbeitens hinweg ist auch wichtig für Abschlussarbeiten. Der folgende Vorschlag für einen Test zum Abschluss der Klasse 10 (vgl. Welt der Zahl, Band 10) wurde in einem Seminar an der Universität Bonn erstellt. Der Test wurde in zwei 10. Klassen von Hauptschulen (N=39), in einer Klasse an einer Gesamtschule (N=22) und zwei Klassen eines Gymnasiums (N=56) erprobt. Ergebnisse werden wegen der niedrigen Probandenzahlen von insgesamt 117 nicht angegeben. Eine Aufgabe in einer Klausur für die Zusatzprüfung für die Sekundarstufe I im Rahmen der 1. Staatsprüfung für das Lehramt Sekundarstufe II bestand darin, die Testaufgaben zu lösen und nach den PISA-Typen zu klassifizieren.

Test zum Abschluss der Klasse 10

1. Ergänze: a) 2,5 · 8 = _____ b) 3,75 + ______ = 10 c) _____ : 0,5 = 12 d) 1 Million : ______ = 10
2. Berechne: a) 1 + 3 · (6 - 4) = b) 10 - 3 · (2 - 1) =   c) =        d) =
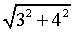3. Ergänze: a) 9² = ___ b) ¿ ² = 49 Wie groß ist x? c) d)
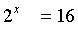
4. Vereinfache: =
5. Arbeite mit der Gleichung y = 9x - 5. a) Welchen Wert hat y für x = 2? y = ____________
   b) Welchen Wert hat x für y = 50? Schreibe auf, wie du rechnest.
6. Löse die Gleichung. Gib alle Lösungen an, wenn es mehrere gibt.
   a) 2x - 10 = 6 Lösung(en): _____________ b) x² - 5x = 0 Lösung(en): _____________
7. Löse die Formel nach x auf.
8. Setze die Zahlenreihe um zwei weitere Zahlen fort:
   a) 7, 9, 12, 16, 21, ____, _____ b) -10, -7, -4, -1, ___, ____ c) 8, 4, 2, 1, ___, ___
9. Ergänze: a) ½ kg = ____ g b) 1 m² = _____ cm² c) 0,5 m³ = _____ l (Liter)
10. Jan benötigt mit dem Fahrrad 10 Minuten für 2,5 km.
    a) Wie groß ist die Durchschnittsgeschwindigkeit in Kilometer pro Stunde?
    b) Wie lange braucht Jan für 27,5 km?
    c) Alexa braucht für den 3 000-m-Langlauf 12 ½ Minuten. Ist ihre durchschnittliche Geschwindigkeit größer als die von Jan? Schreibe auf, wie du rechnest.
11. Ein Rechteck hat einen Flächeninhalt von 20 m². Länge und Breite des Rechtecks ( in Meter ) sind "ganze" Zahlen. Welchen Umfang kann das Rechteck haben? Gib alle Möglichkeiten an.
12. Eine Fabrik stellt Glasflaschen her. Manche haben Fehler. Stelle eine Frage und beantworte sie.
    a) Von 8 000 Flaschen waren an einem Tag 2 % fehlerhaft.
    b) An einem anderen Tag hatten 270 Flaschen einen Fehler, das waren 3 % der Tagesproduktion.
    c) Durchschnittlich werden am Tag 8 000 Flaschen hergestellt, von denen 240 fehlerhaft sind.

Eine Zeitung berichtet über Unfälle von Schülerinnen und Schülern auf dem Schulweg. a) Die Zeitung meldet: "Von allen, die auf dem Schulweg mit dem Rad verunglückten, sind 70% Jungen." Stimmt das mit den Angaben in der Tabelle überein? Begründe. b) Die Zeitung meldet auch: "Jungen sind beim Radfahren gefährdeter als Mädchen!" Stimmt das? Begründe deine Antwort.

Schulweg davon mit Fahrrad verunglückten ____________________ Jungen 1 000 140 Mädchen 300 60 ____________________________ Insgesamt 1 300 200

Mira hat eine kleine Tour mit dem Fahrrad gemacht. Mehrmals hat sie die Fahrzeit und den Kilometer-Stand des Tachometers notiert. Die Kurve zeigt, wie viel Kilometer Mira nach dem Start gefahren ist. a) Wie weit ist sie nach 20 Minuten gefahren? b) Fuhr Mira in den nächsten 20 Minuten schneller oder langsamer als vorher? Begründe deine Antwort. c) Nach 40 Minuten Fahrzeit machte sie eine Pause. Wie lange dauerte die Pause? d) Vergleiche die durchschnittliche Geschwin-digkeit, mit der Mira vor der Pause fuhr, mit der Durchschnittsgeschwindigkeit nach der Pause. Schreibe auf, wie du das machst.

Skizze; nicht maßstabsgetreu

Die Die Skizze zeigt ein gleichschenkliges Dreieck. a) Wie groß sind die Winkel ? b) Welchen Flächeninhalt hat das Dreieck? c) Bestimme den Umfang des Dreiecks. Du kannst dazu eine KKonstruktion des Dreiecks anfertigen. Du kannst die Aufgabe aber auch mmithilfe von einem wichtigen "Satz" ohne Konstruktion lösen.




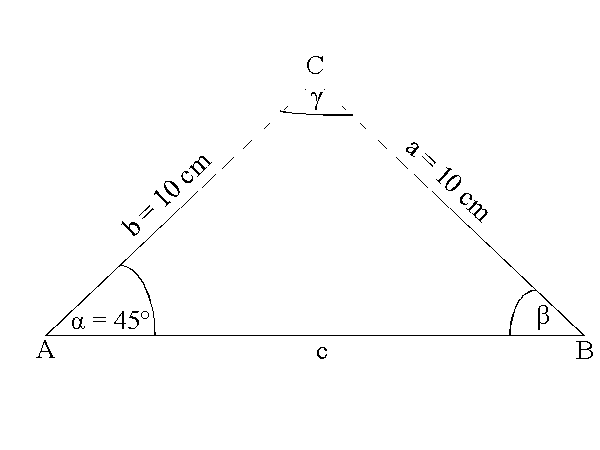
Ein Werkstück aus Aluminium (1cm3 wiegt 2,7 g) besteht aus einem Kegel (Körperhöhe h = ...), der pass-genau auf einer Halbkugel (Durchmesser d =...) steht. a) Wie viel Kilogramm wiegt das Werkstück? Runde auf 2 Stellen nach dem Komma. b) Wie ändert sich das Gewicht des Werkstücks, wenn die Kegelhöhe und der Kegeldurchmesser verdoppelt werden?

Skizze und Formeln sind gegeben.

Wir halten solche Verbindungen von schulbezogenen Aufgaben zur Reflexion innerhalb der Lehrerausbildung für notwendig gerade in Hinblick auf die nun anstehenden Diskussionen um "Standards". Denn produktive Standards wird es nur geben, wenn sie nicht nur Minimalkenntnissen folgen, sondern ein "Kompetenzmodell" als Basis nehmen, wie es auch die Expertise von Klieme (2003) fordert. Gerade von mathematik-didaktischer Seite aus ist dies mit Nachdruck zu unterstützen (Neubrand 2003). Die PISA-Klassifikation stellt ein solches Kompetenzmodell dar (vgl. Neubrand & al. 2002).

Literatur